ما هي أهم أنواع المقاييس الإحصائية؟

تمتلك المقاييس الإحصائية دور هام وفعال في البحث العلمي حيث يتم استخدامها كقواعد أساسية للتأكد من مدى ملائمة النتائج مع الهدف الأساسي. كما تعتبر المقاييس الإحصائية معايير تستخدم للتقييم الكمي ومقارنة الأداء. 

 

وسنتعرف من خلال هذا المقال على كافة المعلومات بخصوص المقاييس الإحصائية، أهميتها وأنواعها، وتعريفها؛ فمن الضروري لك كباحث أن تقرأ بدقة هذا المقال فسيحقق لك الكثير من الاستفادة. 

 

المقاييس الإحصائية هي مجموعة من العمليات الإحصائية، استخدامها الرئيسي هو تحليل كافة البيانات؛ وذلك للمساعدة في التوصل إلى مجموعة من النتائج الخاصة برسالة الماجستير والدكتوراه، ويتم إجراء مجموعة من العمليات الحسابية من خلال أدوات المقياس وجمع البيانات ومن ثم البدء في خطوات العمليات الحسابية الإحصائية.

 

1-تعتبر من أهم الأدوات الفعالة والمفيدة للبحث العلمي.

2-تستخدم كقواعد أساسية لمعرفة هل تتلاءم النتائج مع الأهداف.

3-تستخدم المقاييس الإحصائية في عملية التقييم الكمي للبيانات.

4-تستخدم بشكل أساسي في مقارنة الأداء الخاص بالبيانات في البحث.

 

تعرف أكثر على أهمية القياس في البحث العلمي من خلال هذا المقال.

 

 

يمكن تصنيف المقاييس الإحصائية التي تستخدم في التحليلات الإحصائية كالتالي:

1-مقاييس النزعة المركزية: مثل المتوسط، الوسيط والمنوال.

2-مقاييس التشتت: كالمدى، الانحراف، والانحراف المعياري.

3-مقاييس الارتباط:  مثل الارتباط، الانحدار والتحليل الإحصائي.

4-تحليل التباين: تحليل تباين أحادي وثنائي، التحليل المتعدد وتحليل التقارير.

 

1-مقاييس النزعة المركزية- Measures of Central Tendency

تستخدم مقاييس النزعة المركزية في وصف نقطة التجمع الخاصة بكافة المشاهدات، وقام بابتكار هذه المقاييس الباحث الإنجليزي فرانسيس، وسنتعرف أكثر على هذا النوع من المقاييس من خلال الآتي:

 

أولًا: الوسط الحسابي - Average

يعتبر الوسط الحسابي أحد أنواع المقاييس الإحصائية، ويتم حسابه من خلال حساب المجموع الخاص بالمشاهدات في المتغير الواحد، وبعد ذلك نقوم بقسمة الناتج على المجموع الخاص بعدد مرات المشاهدة لهذا النوع من المتغيرات.

 

ما هي مميزات الوسط الحسابي؟

1-يعتبر أحد المقاييس الإحصائية التي يتم حسابها بطريقة بسيطة وواضحة.

2-يأخد الوسط الحسابي كافة القيم بعين الاعتبار عند إجراء العمليات الحسابية.

3-يعتبر من أكثر المقاييس الإحصائية استخدامًا لسهولته، وفهمه.

 

ما هي عيوب الوسط الحسابي؟

1-تؤثر طبيعة القيم الطرفية على معادلة حساب الوسط الحسابي.

2-يتم استخدام الوسط الحسابي لحساب البيانات الوصفية فقط.

3-من الصعب التعامل مع الوسط الحسابي، لأنه يتطلب منك أن تعرف مركز كافة الفئات.

 

مثال على حساب الوسط الحسابي

يتم حساب الوسط الحسابي من خلال مجموعة كافة القيم / عددها، وسنوضح مثالًا عمليًا على حساب الوسط الحسابي من خلال الآتي:

 

احسب الوَسط الحِسابي للقيم الآتية: (8، 11، 3، 6، 22)

أولًا: اجمع القيم جميعها: 8+11+3+6+22 = 50.

ثانيًا:احسب العدد الخاص بهذه القيم وهو 5.

التَطبيق عَلى القانون: الوَسط الحِسابي= مجموع القيم/عددها.

الوَسط الحِسابي = 5/50 وقيمته 10.

 

 

ثانيًا: الوسيط

يعتبر الوسيط كذلك أحد المقاييس الإحصائية التي تندرج تحت فئة مقاييس النزعة المركزية، ويمكن تعريفه بأنه القيمة التي توجد في منتصف القيم، ومن خلال الوسيط يتم تقسيم كافة القيم إلى نصفين، وكل من النصفين متساويين.

 

 

ما هي مميزات الوسيط؟

1-لا يتأثر الوسيط بأي حال من الأحوال بالقيم المتطرفة.

2-يتم التعامل مع الوسيط إذا كانت البيانات وصفية.

3-يتم الإعتماد عليه في حالة الجداول التكرارية.

 

ما هي عيوب الوسيط؟

1-لا يأخذ الوسيط في اعتباره كافة القيم عندما يتم حسابه.

2-ستجد صعوبة في التعامل مع الوسيط عند إجراء التحاليل الرياضية.

 

خطوات حساب الوسيط

1-يقوم الباحث في بداية الأمر بتجميع القيم الخاصة بالمشاهدات.

2-ترتيب كافة القيم بشكل تصاعدي أو بشكل تنازلي.

3-إذا كان العدد الخاص بالمتغيرات زوجي، نأخذ القيمتين في المنتصف، ونقسم الناتج على 2 لتحديد رتبة الوسيط.

4-إذا كانت القيمة الخاصة بالمتغيرات رقمًا فرديًا، ستكون القيمة الخاصة بالوسيط في هذه الحالة هي القيمة المتواجدة في الوسط.

 

مثال على حساب الوسيط

سنتناول من خلال هذه الفقرة مثال عملي لكيفية حساب الوسيط، وذلك إذا كان عدد القيم الخاصة بالبيانات فرديًا، ويتم الحساب من خلال الآتي:

 

في حالة أن الوسيط هو رقم فردي، فإن الوسيط سيكون القيمة في المنتصف

 

رتبة الوسيط = (عدد المشاهدات + 1)/ 2

ما هو الوسيط للبيانات الآتية: 5، 6، 8، 1،7

 

خطوات الحل

أولًا:نُرتب البيانات من الأصغر للأكبر على النحو الآتي: 1، 5، 6، 7، 8

 

ثانيًا:قم بحساب العدد الخاص بالبيانات وهو 5.

 

ثالثًا:قم بتحديد المكان الخاص بالوسيط أو رتبته.

 

رتبة الوسيط = (عدد المشاهدات + 1)/ 2 رتبة الوسيط = (5+1)/ 2 = 6/2 = 3 رتبة الوسيط = 3، وبذلك فإن الوسيط هو القيمة الثالثة وهي العدد 6.

 

بإمكانك أن تقرأ كذلك عن البيانات الإحصائية من هنا.

 

ثالثًا: المنوال

يعتبر المنوال هو القيمة التي تتكرر عدد كبير من المرات، أو القيمة الأكثر تكرارًا بين كافة البيانات، ويوجد للمنوال الكثير من التصنيفات سنذكرها من خلال الآتي:

 

تصنيفات المنوال

يعتبر المنوال أحد المقاييس الإحصائية المتعلقة بمقاييس النزعة المركزية، ويحتوي المنوال على العديد من التصنيفات، ومن أهم هذه التصنيفات ما يلي:

 

1-عديم المنوال

من الممكن ألا تحتوي القيم على المنوال، وذلك إذا تساوى العدد الخاص بتكرار القيم مع بعضها البعض.

 

2-وحيد المنوال

من الممكن أن تجد كذلك أن القيم الخاصة بالبيانات المتوافرة معك منوالًا واحدًا، وبذلك تكون كافة هذه القيم وحيدة المنوال.

 

3-متعدد المنوال

من الممكن أن تجد أكثر من منوال في القيم الخاصة بك، بمعنى أنك ستجد أكثر من قيمة تساوت في عدد مرات التكرار، وزادت مرات تكرار هذه القيم عن القيم الأخرى.

 

ما هي مميزات المنوال؟

1-من السهل أن يتم حساب المنوال، وكذلك من السهل إيجاده.

2-يتم حساب المنوال لمجموعة كبيرة من البيانات التي تمتلك توزيعات مختلفة.

 

ما هي عيوب المنوال؟

1-لا يراعي المنوال كافة القيم التي يحصل عليها الباحث.

2-سيؤدي انعدام المنوال إلى إعطاء قيمة صفرية.

 

مثال على حساب المنوال

قم بحساب المنوال لحساب لمجموعة الأعداد الآتية: (19, 8, 29, 35, 19, 28, 15) عليك أن تقوم أولًا بترتيب كافة البيانات هكذا (8, 15, 19, 19, 28, 29, 35) والمنوال هو العدد 19، المتكرر مرتين هنا.

 

بإمكانك أن تتعرف أكثر على مقاييس النزعة المركزية من خلال هذا المقال.

 

2-مقاييس التشتت

تعتبر مقاييس التشتت كذلك أحد المقاييس الإحصائية التي تستخدم كثيرًا لتحليل البيانات وللحصول على النتائج،ومن أهم مقاييس التشتت ما يلي:

 

أولًا: المدى - range

يمكن تعريفه على أنه المسافة بين أعلى وأقل العلامات في التوزيع. وللأسف فإن المدى في معظم الأحيان يكون خادعا فهو يعتمد على أعلى العلامات وأقلها، ولا يوجد معلومات عن الوسط (أي ما بين العلامات المتطرفة في الأعلى والأسفل).

 

ما هي مميزات المدى؟

-سهل الفهم.

-سهل الحساب.

-مستقل بذاته.

 

 

ما هي عيوب المدى

-لا يعتبر مقياسًا موثوقًا لحساب التشتت.

-يعتمد اعتمادًا كليًا على تغيير المقياس.

 

مثال على حساب المدى

البيانات هي 4، 6، 9، 3، 7 والمطلوب إيجاد المدى.

 

خطوات الحل

أولًا عليك أن تقوم بترتيب كافة القيم، وفي هذه الحالة، أقل قيمة هي 3، وأعلى قيمة هي 9، لذلك: المدى = 9 – 3 = 6

 

المدى التربيعي

المدى الترييعي هو نوع من المدى. يتجنب بعض المشكلات التي تحصل في المدى بأن يأخذ في الاعتبار وسط الحالات (50% من الحالات) في التوزيع. ولإيجاد المدى الربيعي نتبع الخطوات التالية:

 

- ترتيب العلامات من الأعلى على الأسفل.

- تقسيم التوزيع إلى أرباع.

 

بإمكانك أن تقرأ عن المتغيرات الإحصائية من خلال هذا المقال.

 

ثانيًا: الانحراف المعياري - Standard deviation

كما رأينا فإن محددات المدى والمدى الربيعي كثيرة وفشلهما في استخدام كل العلامات في التوزيع. كما أنهما لا يزوداننا بمعلومات عن المتوسط أو الانحراف عنه. ولذا فإن المقياس الجيد للتشتت الذي نبحث عنه يوفر لنا الجوانب التالية:

 

- استخدام جميع العلامات في التوزيع المعطي.

- يعطينا المتوسط والانحرافات عنه.

- تصبح قيمته أكبر، عندما يصبح توزيع العلامات غير متجانس.

 

والطريقة الوحيدة لتطوير إحصائي يفي بهذه المتطلبات، لا بد أن نجد المسافة بين كل علامة والمتوسط، وجمع هذه المسافات. فالمسافة بين العلامات والمتوسط يطلق عليها أسم الانحراف. ومقياس التشتت يعتمد على هذه الانحرافات.

 

وتزداد قيمة هذه الانحرافات كلما كان توزيع العلامات غير متجانس (لما أصبحت المسافة كبيرة كلما كان مجموع الانحرافات اكبر)، ولسوء الحظ فإن الانحرافات عن المتوسط  لها سلبيتان هما:

 

- إن القياس يزداد بازدياد حجم العينة (كلما ازداد حجم العينة كلما زادت قيمه القياس).

 

- أما السلبية الثانية فهي أن الانحرافات حول المتوسط يكون مجموعها دائما صغيرا، نتيجة طرح القيم السلبية من الموجبة.

 

وفي هذه الحالة يمكن التخلص من الإشارة السلبية بتجاهلها، أو بتربيع الانحرافات أو ما يطلق عليه بالتباين عندما نشير إلى العينة أو الإشارة عندما نشير إلى المجتمع.

 

مثال على حساب الانحراف المعياري

 

طريقة الحل

لحساب الانحراف المعياري يجب أولاً حساب المتوسط الحسابي،

 

المتوسط الحسابي= (مركز الفئة×التكرار)/مجموع التكرارات = (3×6 + 6×10 + 4×14 + 7×18)/ 20 = 13.

 

حساب الانحراف المعياري = [مجموع (التكرار×(مركز الفئة - المتوسط الحسابي)²)/مجموع التكرارات]√،

 

الانحراف المعياري = [(3×(6-13)² + 6×(10-13)² + 4×(14-13)² + 7×(18-13)²)/20]√ = [(147+ 54 + 4 + 175)/20 ]√= 19√ = 4.36.

 

تعرف على كيفية استخدام الاحصاء في البحوث العلمية من خلال هذا المقال.

 

ثالثًا: الانحراف المتوسط - average deviation

يستخدم هذا النوع من أنواع المقاييس الإحصائية في معرفة المتوسط الخاص بانحراف القيم عن المتوسط الخاص بها، ويتم حساب الانحراف المتوسط من خلال الخطوات الآتية:

 

1-نقوم بحساب الوسط الحسابي.

2-نحسب انحراف القيم عن المتوسط الخاص بها.

3-نقوم بتجاهل الاشارات الخاصة بالانحرافات.

4-نقوم بتجميع كافة الانحرافات.

5-نقوم بقيمة المجموع الخاص بالانحرافات على العدد.

 

مثال على حساب الانحراف المتوسط 

 

 

تعرف أكثر على مقاييس التشتت في الإحصاء من خلال هذا المقال.

 

3- مقاييس الارتباط

تعتبر مقاييس الارتباط كذلك أحد أهم المقاييس الإحصائية، وتبرز هذه المقاييس قوة العلاقة بين المتغيرات وبعضها البعض.

 

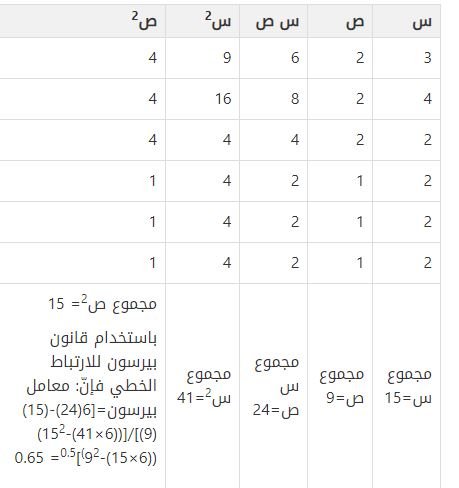
أولًا: معامل الارتباط

ويوجد لهذه المقاييس أنواع كثيرة وأهم نوع هو معامل ارتباط بيرسون، ويستخدم هذا المعامل عند حساب معادلة الانحدار الخطي.

 

كيف يتم حساب معامل بيرسون؟ 

 

 

مثال على حساب معامل الارتباط الخطي بيرسون

 

 

تعرف أكثر عن معامل الارتباط في الاحصاء من خلال هذا المقال.

 

ثانيًا: التحليل الإحصائي

بعد الانتهاء من التحليل الأولى للبيانات، فإن على الباحث الآن أن يأخذ بالاعتبار الإجراءات الإحصائية  وهذه المرحلة من التحليل ترتكز على بعض النماذج الاحتمالية والاختبارات الإحصائية.

 

الغرض من الاستدلال الإحصائي واستخدام الاختبارات الإحصائية هو لإعطاء نتائج من البيانات التي استخدمت في العينة. وعند اختيارنا للاختبار الإحصائي فإن عدة أمور يجب أن تؤخذ بالاعتبار ومنها:

 

- كيف سيتم جمع البيانات.

- ما هو تصميم الدراسة.

- ما هي المقاييس التي ستستخدم.

- متغيرات الدراسة.

- النموذج الإحصائي.

- قوة الإحصائي وعلاقتها بتصميم الدراسة.

 

كيف نتوصل إلى القرار المتعلق بأهمية التحليل الإحصائي المستخدم؟

إن الاستدلال الإحصائي المستخدم في فحص الفرضيات يرتكز على نظرية الاحتمالات، فالاختبار الدال هو الاختبار الذي يجري للفرضية الصفرية وتعد النظرية الاحتمالية مركزية في الاستدلال الإحصائي والاختيارات الإحصائية لأنها تتمكن من معرفة التباين بالصدفة عند اتخاذ القرار.

 

تعرف أكثر عن التحليل الإحصائي في البحث العلمي من خلال هذا المقال.

 

3-تحليل الانحدار

يعتبر تحليل الانحدار كذلك من أهم المقاييس الإحصائية المتشعبة من مقاييس التشتت، وهو عبارة عن طريقة إحصائية تستخدم للتنبؤ بالمتوسط الخاص بالمتغير العشوائي، أو عدة متغيرات عشوائية.

 

أنواع تحليل الانحدار

-الانحدار الخطي.

-الانحدار اللوجستي.

-انحدار بواسون.

 

تعرف أكثر عن الأساليب الإحصائية في البحث العلمي من خلال هذا المقال.

 

4-تحليل التباين

يعتبر تحليل التباين العنصر الرابع والأخير من أنواع المقاييس الإحصائية، ويقوم بدراسة العلاقة بين المتغير الكمي، ومتغير آخر، ما رأيك أن نتعرف على أهم مميزات وعيوب تحليل التباين؟

 

مميزات تحليل التباين

1-المساهمة في إدارة المخاطر.

2-المساهمة في تحديد المخاوف.

3-التغلب على المخاوف.

4-إجراء التغييرات في استراتيجية العمل.

 

عيوب تحليل التباين

1-تأخير الوقت.

2-صعوبة الحصول على مصدر التباين.

3-صعوبة إجراء التحليل التفصيلي.

 

بإمكانك أن تتعرف على المزيد من المعلومات عن خطوات تحليل التباين من خلال هذا المقال

 

إذا أردت أمثلة عملية ومزيد من المعلومات عن المقاييس الإحصائية بإمكانك ان تضغط على الرابط المقاييس الإحصائية pdf، وستجد فيه الكثير من المعلومات المنظمة عن أنواع المقاييس في البحث العلمي pdf.

 

تعرف كذلك على الاختبارات الإحصائية في البحث العلمي من خلال هذا المقال.

 

 

نأمل بأنك استفدت من قراءة مقالنا، وأنك قد تعرفت على كافة المعلومات بخصوص المقاييس الإحصائية، وإذا رغبت في الحصول على خدمات البحث العلمي مثل التحليل الإحصائي وغيرها، اعتمد على موقع إعداد بحوث علمية ( مكتبتك ) وتواصل الآن من خلال الواتساب الخاص بنا. 

 

- الضامن، منذر. (2007). أساسيات البحث العلمي. عمان: دار المسيرة للنشر والتوزيع والطباعة