شرح مفصل عن الاختبارات الإحصائية في البحث العلمي

يحتاج الباحثون الذين يقومون باعداد رسائل الماجستير والدكتوراه إلى مجموعة من الإجراءات تساعدهم على تحليل البيانات والتوصل إلى النتائج، وتلعب الاختبارات الإحصائية في البحث العلمي دور فعال وهام في تحليل البيانات التي يتم جمعها لكي يتم عرضها بصورة دقيقة، وتهدف الاختبارات الإحصائية إلى الوصول للنتائج الصحيحة والتي لها أن تُعَمَّمْ النتائج على المستوي المجتمعي، تعرف أكثر على هذه الاختبارات الآن!

 

الاختبارات الإحصائية في البحث العلمي التي يعتمد تحليلها الإحصائي على التوزيع الطبيعي في البحث العلمي يطلق عليها اسم الإحصاء البارامتري ويجب أن يتحقق في هذا الإحصاء كي يتم تحليله الجوانب التالية:

 

- الملاحظات المستقلة

- يتم سحب العينات من مجتمع الدراسة.

- يتوفر فيها المستوى المتصل من القياس. 

- ترتبط الأخطاء العشوائية بملاحظات ومقاييس لها توزيع معروف (توزيع طبيعي في العادة).

 

أما الاختبارات اللابارامترية فيطلق عليها مصطلح التوزيع الحر وهي تشير إلى استخدام الاختبارات الإحصائية التي لا تعمل افتراضات حول توزيع الأخطاء. وهذه الاختبارات أقل قوة من الاختبارات البارامترية والإستراتيجية البديلة لاستخدام الاختبارات اللاباراميترية أو اللامعلمية، كما يطلق عليها يكون بتحويل البيانات إلى توزيع طبيعي أو قريبا منه.

 

النماذج الإحصائية التي يلجأ إليها الباحث

والباحث في التربية وعلم النفس يلجأ إلى ثلاثة نماذج في دراسته وهي:

- النموذج البارامتري العام  وهذا يعتمد على التوزيع الطبيعي.

- Binomial Model ويعتمد على توزيع binomial.

- التوزيع الحر للإجراءات ويعتمد على التوزيع اللابارامتري.

 

للاختبارات الإحصائية أهمية كبيرة، وسنتعرف عليها من خلال مجموعة من النقاط أهمها ما يلي:

 

1-تساهم الاختبارات الإحصائية في البحث العلمي في تحليل كافة البيانات.

2-المساهمة في عرض جميع البيانات بصورة دقيقة وبسيطة.

3-التوصل إلى مجموعة من النتائج الصحيحة الخاصة بالمستوى المجتمعي.

 

تعرف كذلك على أهمية الأساليب الإحصائية في البحث العلمي من خلال هذا المقال.

 

إذا أردت أن تقوم بخطوات الاختبارات الإحصائية في البحث العلمي بشكل صحيح بإمكانك أن تقوم بمجموعة من الخطوات، وسنتعرف على هذه الخطوات من خلال هذه الفقرة، أهم خطوات الاختبار الإحصائي:

 

 

أولًا: صياغة السؤال البحثي والمحتوى الخاص به

قبل القيام بباقي خطوات الاختبارات الإحصائية في البحث العلمي يجب عليك كباحث أن تقوم بصياغة السؤال الخاص بالبحث؛ وينبغي أن تقوم بصياغة كافة الأسئلة البحثية التي يتمكن الباحث من خلالها من  إثبات أو نفي الفرضية البحثية.

 

وإذا وجد الباحث أحد الأسئلة التي تحتوي على تساؤلات كثيرة؛ فينبغي أن يقوم الباحث بتقسيم هذه الأسئلة الرئيسية إلى مجموعة من الأسئلة الفرعية، فما رأيك أن نوضح ذلك من خلال مثال بسيط.

 

مثال يوضح صياغة الأسئلة البحثية

إذا أراد الباحث على سبيل المثال أن يختبر التأثير الكبير للساعات التي يتم مشاهدة الإعلام فيها على المتوسط الخاص بعمر الإنسان، وكذلك إذا أراد الباحث أن يقوم بقياس مدى التأثير على متوسط العمر الزمني للرجال والنساء، ففي هذا المثال سيتعين على الباحث القيام بالآتي:

 

-اختبار مدى تأثير مشاهدة جميع الإعلام على المتوسط الخاص بعمر الإنسان.

-من ثم سيحتاج إلى استخلاص جميع النتائج ليتمكن من الإجابة على السؤال التالي.

-الإجابة على التساؤل الذي يوضح تأثير مشاهدة الإعلام على متوسط عمر الرجال.

-الإجابة على التساؤل الذي يوضح تأثير مشاهدة الإعلام على متوسط عمر النسائي.

 

ويجب على الباحث أن يبدأ في التفكير في الآلية الصحيحة للإجابة على هذا التساؤل الخاص بالبحث، وإذا توجب الأمر إجراء مجموعة من الاختبارات الإحصائية للإجابة على هذه التساؤلات يجب أن يقوم الباحث بذلك.

 

ثانيًا: إعداد الفرضيات الإحصائية الخاصة بالبحث

ويوجد نوعان من الفرضيات الإحصائية التي يقوم الباحث بإعدادها عند عمل الاختبارات الإحصائية في البحث العلمي في رسائل الماجستير والدكتوراه الخاصة بالباحث، وهذان النوعان من الفرضيات كالتالي:

 

1-فرض العدم، ويعتبر فرض العدم عبارة عن فرض يتم صياغته في حالة عدم وجود تأثير أو علاقة بين المتغيرات الخاصة بالبحث، ويرمز لهذا النوع من الرموز بـ ( H0 ).

 

2-الفرض البديل، ويسمى كذلك بالفرض التجريبي، ويحتوي هذا النوع من الفروض على قيمة صحيحة، ويتم حساب هذا النوع من الفروض في حالة أن الفرض المسمى بالعدم غير موجود، ويطلق عليه ( H1 ).

 

مثال يوضح فرض العدم والفرض البديل

فرض العدم ( H0 ) يظهر ذلك عندما لا يوجد أي تأثير تسببه ساعات المشاهدة الخاصة بالإعلام على العمر الخاص بالإنسان.

 

الفرض البديل ( H1 ) عند وجود تأثير واضح أو علاقة قوية بين ساعات مشاهدة الإعلام وكذلك على المدى الخاص بمتوسط العمر الزمني الخاص بالإنسان.

 

ثالثًا: اختيار العينة الخاصة بالبحث العلمي

وفي هذه الخطوة سيتم اختيار عينة إحصائية تحتوي على مجموعة من الرجال وكذلك النساء، وبالتطبيق على المثال الوارد ذكره، سيتم اختيار عينة تشاهد الإعلام، وذلك للحصول على المعلومات أو البيانات من خلالها.

 

رابعًا: اختيار طريقة جمع البيانات في الدراسة

توجد الكثير من الطرق الخاصة بجمع البيانات في البحث العلمي، ويجب على الباحث أن يختار طريقة منهم الطريقة المناسبة، ويتم الاختيار بناءً على نوع البيانات التي يرغب الباحث العلمي في جمعها.

 

وإذا رغبنا في توضيح ذلك بمثال، سنستخدم المثال السابق ذكره، وفي هذه الحالة سيتم جمع بيانات بخصوص الساعات المخصصة لمشاهدة الإعلام، ويعتبر هذا النوع من البيانات ( بيانات كمية ) كما يعتبر كل من الجنس والعمر ( بيانات وصفية ).

 

خامسًا:اختيار طريقة الاختبار الإحصائي

يتم اختيار طريقة الاختبارات الإحصائية في البحث العلمي من خلال مجموعة من النقاط، ويجب أن تأخذ في بالك مجموعة من المعايير لتختار الاختبار الملائم، وكافة الاختبارات الإحصائية تقبل مجموعة من الأنواع المحددة الخاصة بالبيانات، ويجب أن تتأكد أن نوع الاختبار الإحصائي الذي اخترته ملائمًا تمامًا لنوع البيانات التي جمعتها.

 

بإمكانك أن تتعرف كذلك على طريقة اختبار الفروض في البحث العلمي من خلال هذا المقال.

 

وإذا أراد الباحث أن يختار الاختبار الإحصائي المناسب فإن عليه مراعاة ما يلي:

 

- السؤال البحثي: إذ يتوجب على الباحث أن يسأل نفسه هل السؤال البحثي الرئيسي يهتم بالعلاقة، أو بالتنبؤ بين المقاييس، أو بالمقارنة بين المجموعات.

 

- تصميم البحث: كم مجموعة ستشملها الدراسة وهل يوحد علاقة بين هذه المجموعات؟ هل يوجد مجموعتان أو أكثر ترتبطان ببعضهما أو مستقلتان؟

 

- توزيع البيانات: هل التوزيع للمتغيرات الهامة منفصلا أو متصلا.

 

الأسئلة البحثية  (الارتباط)

كثير من الدراسات البحثية يطرح فيها أكثر من سؤال بحثي، لذا فإنه يستخدم أكثر من نوع من الاختبارات الإحصائية. فإذا كان الغرض من الدراسة هو فحص العلاقة بين المفحوصين فإن الارتباط سيكون هو الإحصاء المستخدم.

 

ومعامل الذكاء يعطينا مؤشر على قوة العلاقة بين متغيرين. حتى أن علاقة الارتباط الضعيفة (معامل ارتباط ضعيف) يمكن أن يعطينا دلالة إحصائية إذا كان حجم العينة كبيرا. وإذا كانت البيانات مرتبطة تصنيفا فإن معادلة سبيرمان هي المناسبة. وإذا كانت البيانات متصلة وموزعة توزيعا اعتداليا فإن معامل ارتباط بيرسون هي التي يجب أن تستخدم.

 

أما الإحصائي  أو اختبار الاستقلالية وما يطلق عليه فهو يشير إلى الحد الذي تكون فيه التكرارات الملاحظة مرتبطة بالمتوقعة. وهذا المقياس يقيس العلاقة بين متغيرين يتضمنان تصنيفين أو أكثر إذن يعد هذا المقياس مناسب إذا احتوي تصنيفين أو أكثر على متغيرين. 

 

وتكون النظرية الصفرية (انه لا يوجد علاقة بين المتغيرين) فهما مستقلان. وإذا استخدمنا عينتين ففي هذه الحالة تستخدم  اختيار التجانس حيث تشير إلى عدد التصنيفات في حين نشير إلى مجتمعي الدراسة.

 

الاعتماد والتنبؤ

إذا كانت الأسئلة البحثية ترتكز على التنبؤ، ففي هده الحالة يمكن أن نستخدم تحليل الانحدار، والشكل البسيط منه يطلق عليه الانحدار الخطي حيث يكون المتغير معتمدا على المتغير المتنبأ  وإن كلا المتغيرين متصلان وبينهما علاقة خطية، ويمكن استخدام معادلة الانحدار بالتنبؤ. إذا كان هماك متغير تابع لأكثر من متغير مستقل فإننا نستخدم الانحدار المتعدد.

 

الفروق بين نوعيتين

عندما تصمم الدراسة للحديث عن عينتين فإنه يتبادر إلى الذهن اختبار ت ويطلق عليه أحيانا (المقارنة بين مجموعتين) مثال إيجاد متوسط الطول عند الذكور والإناث. وذلك لمعرفة إذا كانت الفروق بينهما دالة إحصائيا. وتكون النظرية الصفرية لاختبارات المستقل.

 

إذا كان هناك أكثر من عينتين تجري المقارنة بينهما وكان التوزيع طبيعيا فإننا نستخدم في هذه الحالة تحليل التباين كما نستخدم اختبار ف وهو مقياس معلمي له خصائص متشابهة لمقياس ت والنظرية الصفرية المستخدمة في هذا المقياس.

 

مصدر التباين 

إن تصميم العينة الجيدة يقلل من كمية التباين في العينة المدروسة أو في الأدوات لمستخدمة إلى مستوى يحقق الغرض من الدراسة. والتباين موجود في أدوات الدراسة.

 

فلو أجرينا قياس لظاهرة معينة عند الأطفال اليوم وأعدنا القياس في اليوم التالي فإنه سيكون هناك اختلاف وهذا التباين يعزى إلي التباين العشوائي في الأداة، والى التغير الحقيقي الذي يطرأ لديهم.

 

اختيار الاختبارات الإحصائية

بعد جمع البيانات، نستخدم الإحصاء الوصفي لتلخيص هذه البيانات. واستخدام الإحصاء المناسب يتأثر بطبيعة الأسئلة البحثية وطبيعة البيانات المستخدمة في الدراسة. 

 

وعلى سبيل المثال إذا كانت القيم متركزة على الأطراف فإنا في هذه الحالة نلجأ إلى استخدام الوسيط بدلا من الوسط، لأنه انسب في مثل هذه الحالة وإذا كان المطلوب تقدير الفروق في المتوسط بين مجموعتين مستقلتين فإننا نلجأ إلى استخدام اختبار ت وإذا أردنا أن نقيم برنامجا لنرى التغير الحاصل عند الأفراد.

 

فسيكون قياس الفروق مبنيا على (العلامات القبلية والبعدية) وستكون الفروق في المتوسطات هي الفروق بين القبلية والبعدية.

 

بعد أن ذكرنا تفصيليًا كيفية اختيار الاختبار الإحصائي الملائم، سنكمل الخطوات المستخدمة في اختيار الاختبار الإحصائي الملائم، وذلك من خلال الآتي:

 

سادسًا: تحليل وتفسير جميع البيانات

تعتبر خطوة تحليل وتفسير جميع البيانات من الخطوات الرئيسية الخاصة بـ إجراء الاختبارات الإحصائية في البحث العلمي، وأهمية هذه الخطوة تتضح في الوصول إلى مجموعة من النتائج الصحيحة الخاصة بالدراسة.

 

سابعًا: استخلاص وتفسير نتائج البحث

من خلال هذه الخطوة يتم استنتاج مجموعة كبيرة من الإجابات الخاصة بالأسئلة البحثية الرئيسية، وكذلك الأسئلة الفرعية، وكذلك يتم تفسير جميع النتائج الخاصة بالبحث أو برالة الماجستير والدكتوراه. 

 

تعرف كذلك على الإحصاء الوصفي من خلال هذا المقال.

 

 

سنتناول في هذه الفقرة دليل الاختبارات الإحصائية، والذي يوضح جميع أنواع الاختبارات الإحصائية في البحث العلمي، وسنذكر جميع هذه الأنواع من خلال الآتي:

 

أولًا: اختبار فيتشر للترابط غير العشوائي بين المتغيرات - FISHER TEST

يعمل الباحث في كافة الدراسات الاستقصائية على الربط بين كافة المتغيرات في البحث العلمي، ويوضح كذلك أهم العوامل التي تؤثر على كافة المتغيرات، ويستخدم اختبار فيتشر في إثبات هل العلاقة بين المتغيرات علاقة نمطية أم علاقة عشوائية.

 

ويتم قياس صحة الفرضية الخاصة بالإختبار من خلال (p-value) وكلما اقتربت هذه القيمة من الواحد الصحيح، سيثبت ذلك عدم وجود أي أدلة ضد الفرضية الأساسية الخاصة بالإختبار وتسمى (null hypothesis). 

 

مثال يوضح اختبار فيتشر

يمكن أن يستخدم اختبار فيتشر للتأكد من العلاقة بين عدد المصابين بمرض الإنفلونزا بـ تعاطي المضاد الوقائي الخاص بهذا المرض.

 

ثانيًا: اختبار مربع-كاي ( CHI-SQUARE )

يعتبر اختبار مربع-كاي كذلك أحد أنواع الاختبارات الإحصائية في البحث العلمي، ويستخدم هذا النوع من الاختبارات للتأكد من طبيعة التوزيع الإحصائي الخاص بكافة النتائج.

 

 ويتم ذلك من خلال التباين (variance) ويتم في هذه الحالة عمل مقارنة بين التباين الحقيقي الخاص بالنتائج، وكذلك التباين النظري الخاص بكافة النتائج، ويتم تحديد طبيعة الاختلاف بينهما.

 

مثال على اختبار مربع- كاي

 

 

ثالثًا:اختبار كروسكال-والليز - KRUSKAL-WALLIS TEST

يعتبر اختبار كروسكال كذلك واحدًا من أهم الاختبارات الإحصائية في البحث العلمي، ويستخدم في إجراء مقارنة بين مجموعة كبيرة من النتائج، والقيام بتحديد ما إذا كانت هذه النتائج ستحقق نفس التوزيع الإحصائي أم لا.

 

يتم قياس صحة الفرضية في هذا النوع من الاختبارات من خلال (p-value)، ومن ثم يتم عرض التمثيل الصندوقي (Box-plot)، وذلك لمقارنة القيمة الوسطى، وكذلك التوزيع الإحصائي بشكل يمثل النتائج الخاصة بالمجموعات

 

مثال على اختبار كروسكال

 

 

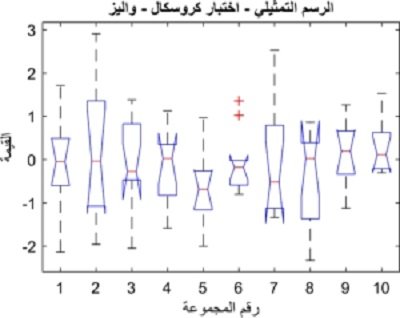
اختبار تحليل تباين-الانحدار لمجموعة من النتائج

يستخدم هذا النوع من الاختبارات الإحصائية في إجراء دراسة دقيقة توضح مدى العلاقة التي تتم بين متغيرين، وتوضح التأثير الكبير الخاص بالمؤثرات الخارجية على هذا النوع من العلاقات.

 

مثال على اختبار تحليل التباين

سنوضح مثالًا لجدول تم رصد فيه العلاقة بين المتغير ( X ) والمتغير ( Y )، وتم تسجيل النتائج الخاصة بهذه المتغيرات على مدار ثلاثة أيام وتم إدراجها في جدول كالتالي:

 

 

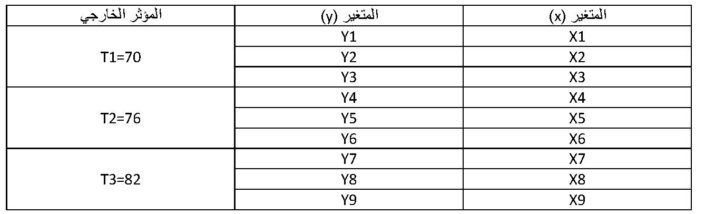
وبعد الإنتهاء من رصد النتائج في جدول يتم تمثيل البيانات من خلال رسم بياني يظهر كالتالي:

 

 

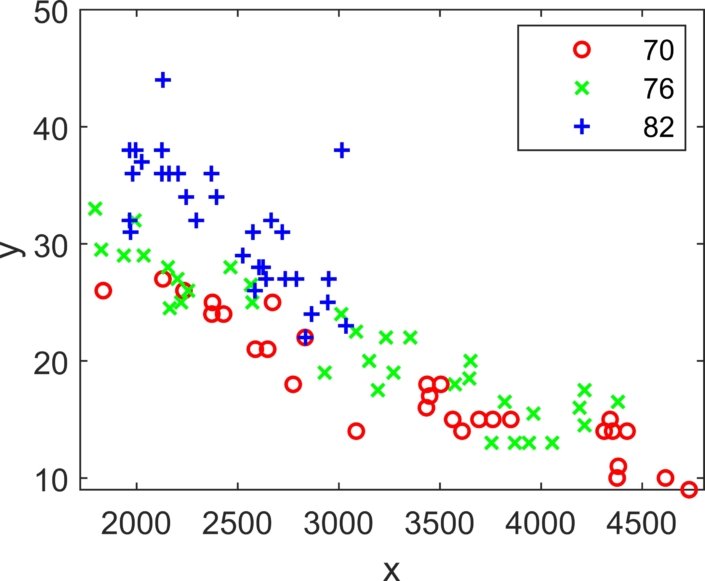
رابعًا: اختبار مقارنة متوسطات النتائج

يعتبر اختبار مقارنة متوسطات النتائج كذلك واحدًا من أنواع الاختبارات الإحصائية في البحث العلمي، ومن خلال هذا الاختبار يتم إجراء تمثيل دقيق لكافة النتائج الخاصة بالبحث، فعلى سبيل المثال النتائج الخاصة بالعينات وغيرها.

 

يتم استخدام القيمة المتوسطة الخاصة بالمدى الإحصائي لإجراء عملية التعير لكافة المعلومات، ومن ثم التعبير عن ذلك برسم بياني أو توضيحي، ما رأيك أن نوضح اختبار مقارنة متوسطات النتائج من خلال مثال؟

 

مثال على اختبار مقارنة متوسطات النتائج

 

 

خامسًا: اختبار فريد مان لإختبار تجانس النتائج

يعتبر اختبار فريدمان، وكذلك اختبار مقارنة المتوسطات متشابهان للغاية، وفي هذا النوع من الاختبارات يتم التعبير عن النتائج الخاصة بالاختبارات بشكل رقمي، ولا يتم الاعتماد على الشكل التمثيلي للنتائج.

 

سادسًا: نموذج دوربن-ويستون لاختبار استقلالية النتائج

يسمى هذا النوع من الاختبارات كذلك باختيار الإنحدار الخطي (Linear regression) وكافة النتائج الخاصة بهذا النوع من الاختبارات مستقلة، ولا تعتمد إطلاقًا على بعضها البعض، ويتم استخدام هذا النوع من النتائج تحديدًا لاختبار الصحة الخاصة بالفرضية.

 

سابعًا: اختبار قياس عدم التبعية

من أنواع الاختبارات الإحصائية في البحث العلمي كذلك اختبار قياس عدم التبعية، وهذا الاختبار يعتبر استخدامه الأساسي تحديد مدى صحة الفرضيات، وكافة النتائج لا تعتمد ولا تتبع فئات معينة.

 

مثال على اختبار قياس عدم التبعية

ومن أهم الأمثلة شرب السجائر، وستجد أنه لا علاقة له على الإطلاق بالتقسيم الخاص بالفئات ( رجال - نساء ).

 

ثامنًا: مصفوفة سبيرمان

يعتبر كلا الاختبارين بيرسون وسبيرمان متشابهان تمامًا، والغرض منهما أن يتم تعيين معامل الارتباط الخطي، ويتم استخدامه مع كافة النتائج التي تتميز بأنها رتبية، ويجب ألا يكون معدل التغير بين كافة المتغيرات ثابت. 

 

تاسعًا: تعيين معامل الارتباط الخطي

يتم استخدام هذا النوع من الاختبارات الإحصائية قبل إجراء اختبار الإنحدار الخطي، ويتم عمل تقييم يوضح مدى تطابق المعادلة الرياضية مع كافة النتائج المعملية، والفرض الأساسي الخاص بهذا الاختبار هو عدم وجود أي علاقة بين المتغيرات.

 

مثال على اختبار تعيين معامل الارتباط الخطي

 

 

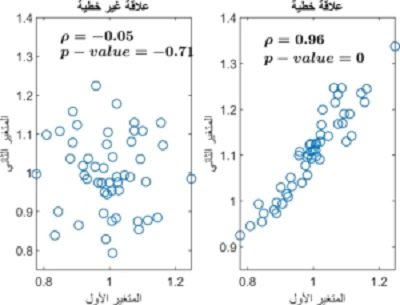
وبذلك نكون قد ذكرنا أهم أنواع اختبارات التحليل الإحصائي، وإذا أردت أن تتعرف على مزيد من الأنواع الخاصة بهذه الإختبارات بإمكانك أن تقرأ دليل الاختبارات الإحصائية وستجد معلومات إضافية.

 

وعليك أن تتعرف على كيفية إدراج الملاحق والجداول والأشكال في البحث العلمي من خلال هذا المقال.

 

إذا أردت أن تطلع على المزيد من المعلومات عن الاختبارات الإحصائية في البحث العلمي، ينبغي عليك أن تقوم بتحميل ملف عن الاختبارات الإحصائية pdf، وستجد الكثير من المعلومات المفيدة في هذا الملف، وإذا أردت كتاب الاختبارات الإحصائية بإمكانك أن تستعين بهذا الرابط.

 

إذا أردت أن تتعرف على الاختبارات المعلمية وكذلك الاختبارات اللامعلمية عليك أن تقرأ الكثير من المعلومات عنها؛ ولذلك تقدم لك شركة مكتبتك ملف عن الاختبارات المعلمية واللامعلمية PDF، قم بتحميله الآن!

 

 

وبذلك نكون قد قدمنا لك معلومات كافية عن الاختبارات الإحصائية في البحث العلمي، وإذا أردت الاعتماد على موقع للخدمات الاكاديمية، بإمكانك أن تعتمد على موقع شركة مكتبتك، وتواصل الآن معنا من خلال الواتساب وسنساعدك بلا شك.

 

- الضامن، منذر. (2007). أساسيات البحث العلمي. عمان: دار المسيرة للنشر والتوزيع والطباعة.